Présentation
Boston GIS (pour Boston Geographic Information Systems http://www.bostongis.com/) est un excellent site que je consulte régulièrement. Il y a environ deux ans, j'ai lu une série de trois tutoriels présentant PL/R. Ces lectures ont fait germer en moi l'idée de la mise en place d'un algorithme de squelettisation de cours d'eau surfacique (POLYGON) dans l'environnement PostGIS.
J'ai mis au point cet algorithme il y a un an, et très récemment en téléchargeant l'extension Skeletonizer 1.0 pour OpenJump , j'ai eu la surprise après la lecture du guide utilisateur de remarquer une approche similaire pour la réalisation de cette fonctionnalité de squelettisation.
Je vais donc vous présenter la mise en place de l'algorithme tel que je l'ai défini, mais je vous invite à étudier celui défini dans le guide utilisateur de Skeletonizer, en sachant que l'équipe de développement est issue de Refractions Research , a qui l'on doit PostGIS, uDig, Geotools, Geoserver.
PostgreSQL/PostGIS quelles versions ?
La version de PostgreSQL que j'utilise est 9.0.1 (32 bit).
La version de PostGIS que j'utilise est la 1.5.2.3 (32 bit).
Qu'est-ce que la Squelettisation ?
La squelettisation consiste à réduire une forme en un ensemble de courbes, appelées squelettes, centrées dans la forme d'origine.
Qu'est-ce qu'est PL/R ?
PL / R est une extension du langage PostgreSQL qui permet d'écrire des fonctions PostgreSQL et des fonctions d'agrégation dans le langage de calcul statistique R.
Qu'est-ce que le langage R ?
R est à la fois un langage ainsi qu'un environnement pour faire de l'analyse statistique. R est disponible en logiciel libre sous licence GPL. Pour ceux qui connaissent des environnements tels que S, MatLab, et SAS - R a le même objectif. Pour plus d'informations sur R consulter le lien suivant :
http://www.r-project.org/
Lien pour chaque tutorial de BostonGIS :
PL/R Part 1
PL/R partie 1 (traduction automatique par Google)
PL/R Part 2 : PL/R and PostGIS
PL/R partie 2 (traduction automatique par Google)
PL/R Part 3
PL/R partie 3 (traduction automatique par Google)
Je vous recommande la lecture de chaque tutorial, mais plus particulièrement :
- le premier (PL/R Part 1) qui vous permettra d'installer R, ainsi que l'extension PL/R.
- le second (PL/R Part 2) qui vous permettra d'installer le package deldir pour R, qui est indispensable pour la réalisation de ce qui va suivre.
Ce package permet de réaliser :
- Une triangulation de Delaunay,
- Un diagramme de Voronoï. C'est cette fonctionnalité que nous allons utiliser.
Un diagramme de voronoï forme une partition de l'espace qui attribue à chaque point une parcelle englobante qui comprend tout l'espace où l'on se trouve plus proche de ce point que de tout autre. Il doit son nom au mathématicien russe Georgi Fedoseevich Voronoï (1868 - 1908).
La figure ci-dessous montre la construction d'un diagramme de Voronoï à partir d'un ensemble de points.
Introduction
Voila le décor est planté nous allons pouvoir passer aux choses sérieuses, dans un premier temps nous allons créer un schéma sous PostgreSQL qui contiendra les fonctions et les tables nécessaire à la réalisation de ce tutoriel. Nous utiliserons PgAdmin III 1.12.1 qui est compatible avec la version de PostgreSQL 9.0, pour la connexion à la base de données et la réalisation de toutes les requêtes.
A la fin de chaque étape de création d'objets géométriques nous visualiserons le résultat sous OpenJump (à télécharger impérativement) dont la dernière version est compatible avec PostgreSQL 9.0. A la fin de ce tutoriel nous verrons comment utiliser le plugin PostGisViewer que j'ai développé pour PgAdmin III, pour réaliser l'enchainement de toutes les requêtes et en visualiser le résultat. Plugin qui a été présenté à ma grande satisfaction dans le Posgres on line journal en même temps que la version 1.13 de PgAdmin III (encore en phase de développement) qui apporte entre autre une nouvelle gestion des plugins, vous pouvez consultez cet article à l'adresse suivante :
http://www.postgresonline.com/journal/archives/180-pgAdmin113plugins_postgis.html
Etape 1 : Création du Schéma
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III et exécutez la
-- Schema: skeleton
-- DROP SCHEMA skeleton;
CREATE SCHEMA skeleton
AUTHORIZATION postgres;
GRANT ALL ON SCHEMA skeleton TO postgres;
GRANT ALL ON SCHEMA skeleton TO public;
Etape 2 : Création de la table avec insertion d'une géométrie
Téléchargez la requête suivante et exécutez la dans l'éditeur de requêtes de PgAdmin III
CREATE TABLE skeleton.water_area...
Visualisation du contenu de la table
Nous allons visualiser le contenu de notre table sous OpenJump, pour cela allez dans le menu Couche
Puis exécuter la requête suivante :
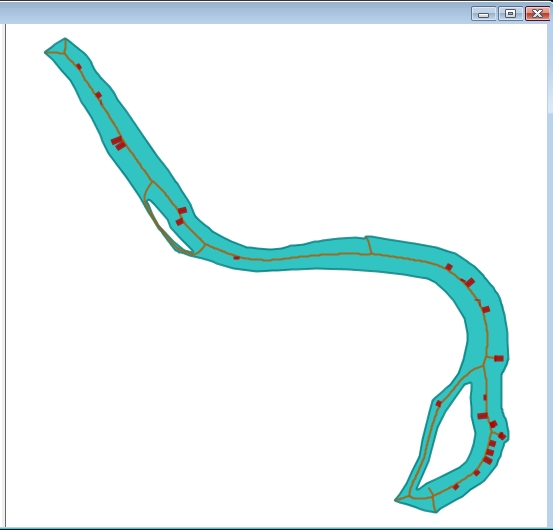
Et voilà à quoi ressemble le polygone que nous allons squelettiser, c'est une partie de cours d'eau avec deux iles, donc nous avons un POLYGON composé de deux « interioring » et d'un « exteriorring ».
Etape 3 : Création des fonctions
Nous allons créer maintenant les fonctions nécessaires au traitement de squelettisation.
1) skeleton.vronoi
Cette première fonction est adaptée de la fonction voronoi tirée du tutorial PL/R Part 2 : PL/R and PostGIS de BostonGis.
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III et exécutez la
/*--- fonction pour créer le diagramme de voronoi ---*/
-- Function: skeleton.voronoi(text, text, text)
CREATE OR REPLACE FUNCTION skeleton.voronoi(text, text, text)
RETURNS void AS
$BODY$
library(deldir)
# select the point x/y coordinates into a data frame...
points <- pg.spi.exec(sprintf("select x(%2$s) as x, y(%2$s) as y from %1$s;",arg1,arg2))
voro = deldir(points$x, points$y, digits=22, frac=0.00000000000000000000000001,list(ndx=2,ndy=2,fctr=0.000001), rw=c(min(points$x)-abs(min(points$x)-max(points$x)), max(points$x)+abs(min(points$x)-max(points$x)), min(points$y)-abs(min(points$y)-max(points$y)), max(points$y)+abs(min(points$y)-max(points$y))))
# dirsgs
for (i in 1:length(voro$dirsgs[[1]]))
{
#--- voronoi ---
pg.spi.exec(sprintf("INSERT INTO skeleton.%1$s (id,idedge,wkb_geometry) VALUES (%2$d,%2$d,GeomFromtext('LINESTRING(%3$f %4$f, %5$f %6$f)',4326));",
arg3,i,
voro$dirsgs[i,1],voro$dirsgs[i,2],
voro$dirsgs[i,3],voro$dirsgs[i,4]))
}
$BODY$
LANGUAGE plr VOLATILE
COST 100;
ALTER FUNCTION skeleton.voronoi(text, text, text) OWNER TO postgres;
GRANT EXECUTE ON FUNCTION skeleton.voronoi(text, text, text) TO postgres;
GRANT EXECUTE ON FUNCTION skeleton.voronoi(text, text, text) TO public;
2) skeleton.sridUtmByLongitude
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III et exécutez la
/*--- fonction pour obtenir le srid UTM zone de la geometrie ---*/
-- Function: skeleton.sridUtmByLongitude(geometry)
CREATE OR REPLACE FUNCTION skeleton.sridUtmByLongitude(geometry)
RETURNS integer AS
$BODY$
DECLARE
gg ALIAS FOR $1; -- Geometrie
pt geometry; -- Geometrie de type POINT
sr int4; -- srid
BEGIN
sr := 0;
IF GeometryType(gg)='POINT' THEN
pt := gg;
ELSE
pt := ST_Centroid(ST_Envelope(gg));
END IF;
sr := SRID(pt);
IF sr = 4326 THEN
SELECT srid into sr FROM spatial_ref_sys
WHERE srtext like
(
SELECT
CASE
WHEN int2(y(pt)) >= 0
THEN '%WGS 84 / UTM zone '||int2((x(pt)+180)/6+1)||'N%'::text
ELSE '%WGS 84 / UTM zone '||int2((x(pt)+180)/6+1)||'S%'
END
AS utmzone
);
END IF;
RETURN sr;
END;
$BODY$
LANGUAGE plpgsql VOLATILE STRICT
COST 100;
ALTER FUNCTION skeleton.sridUtmByLongitude(geometry) OWNER TO postgres;
GRANT EXECUTE ON FUNCTION skeleton.sridUtmByLongitude(geometry) TO postgres;
GRANT EXECUTE ON FUNCTION skeleton.sridUtmByLongitude(geometry) TO public;
3) skeleton.smoothvoronoiline
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III et exécutez la
/*--- fonction lissage ---*/
-- Function: skeleton.smoothvoronoiline(geometry)
-- DROP FUNCTION skeleton.smoothvoronoiline(geometry);
CREATE OR REPLACE FUNCTION skeleton.smoothvoronoiline(geometry)
RETURNS geometry AS
$BODY$
DECLARE
geom ALIAS FOR $1; -- geometry
sql1 text;
rec1 RECORD;
BEGIN
IF ST_NumPoints(geom)>2 THEN
sql1:='SELECT ST_LineFromMultiPoint(ST_Collect(a.geom )) as geom
FROM
(
SELECT ST_PointN(geometry('||quote_literal(geom::text)||'),generate_series(1,ST_NumPoints(geometry('||quote_literal(geom::text)||')),2)) as geom
) a;';
FOR rec1 IN EXECUTE sql1 LOOP END LOOP;
IF FOUND THEN
RETURN ST_AddPoint(rec1.geom,ST_EndPoint(geom));
END IF;
ELSE
RETURN geom;
END IF;
END;
$BODY$
LANGUAGE plpgsql VOLATILE STRICT
COST 100;
ALTER FUNCTION skeleton.smoothvoronoiline(geometry) OWNER TO postgres;
GRANT EXECUTE ON FUNCTION skeleton.smoothvoronoiline(geometry) TO postgres;
GRANT EXECUTE ON FUNCTION skeleton.smoothvoronoiline(geometry) TO public;
Etape 4 : Squelettisation
1) Création du diagramme de voronoï
Paramètre 1 : une liste de points que l'on extrait de l'exteriorring et de chaque interiorring,
SELECT ST_PointN(wkb_geometry,generate_series(1, ST_NumPoints(wkb_geometry))) as geom
FROM
(
SELECT st_exteriorring(wkb_geometry) as wkb_geometry,
ST_Length(ST_Transform(st_exteriorring(wkb_geometry),skeleton.sridUtmByLongitude(wkb_geometry))) as length
FROM skeleton.water_area
) as a
UNION ALL
SELECT ST_PointN(wkb_geometry,generate_series(1, ST_NumPoints(wkb_geometry))) as geom
FROM
(
SELECT ST_InteriorRingN(wkb_geometry,generate_series(1,ST_NumInteriorRings(wkb_geometry))) as wkb_geometry,
ST_Length(ST_Transform(ST_InteriorRingN(wkb_geometry,generate_series(1,ST_NumInteriorRings(wkb_geometry))),skeleton.sridUtmByLongitude(wkb_geometry))) as length
FROM skeleton.water_area WHERE id=1
) as b
Paramètre 2 : la table qui contiendra les lignes composant le diagramme de voronoï.'b.geom','voronoi_line'
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III et exécutez la
SELECT skeleton.voronoi('(
SELECT ST_PointN(wkb_geometry,generate_series(1, ST_NumPoints(wkb_geometry))) as geom
FROM
(
SELECT st_exteriorring(wkb_geometry) as wkb_geometry,
ST_Length(ST_Transform(st_exteriorring(wkb_geometry),skeleton.sridUtmByLongitude(wkb_geometry))) as length
FROM skeleton.water_area
) as a
UNION ALL
SELECT ST_PointN(wkb_geometry,generate_series(1, ST_NumPoints(wkb_geometry))) as geom
FROM
(
SELECT ST_InteriorRingN(wkb_geometry,generate_series(1,ST_NumInteriorRings(wkb_geometry))) as wkb_geometry,
ST_Length(ST_Transform(ST_InteriorRingN(wkb_geometry,generate_series(1,ST_NumInteriorRings(wkb_geometry))),skeleton.sridUtmByLongitude(wkb_geometry))) as length
FROM skeleton.water_area WHERE id=1
) as b
) as b','b.geom','voronoi_line');
Visualisez le contenu la table skeleton.voronoi_line sous OpenJump, pour cela allez dans le menu Couche
Puis exécutez la requête suivante :
Et voici le resultat :
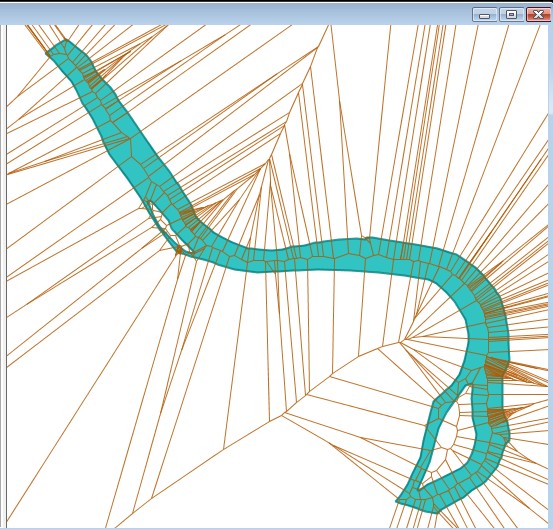
Vous pouvez remarquer qu'au centre du cours d'eau se dessine un squelette, pour le rendre plus visible, exécutez la requête suivante qui va le renforcer.
Le squelette sur le bras le plus étroit n'est pas présent, alors que sur le bras plus large celui est présent. A ce stade du tutoriel, il semblerait que la squelettisation de ce cours d'eau n'est pas sur la bonne voie….
Pourtant rien n'est perdu, en analysant la figure ci-dessus, il apparait que la densité de points n'est pas assez importante, PostGIS va nous fournir la fonction qui va permettre d'augmenter cette densité, et plus précisément de placer des points sur le contour extérieur ainsi que les contours intérieurs avec un espacement déterminé.
Cette fonction est la fonction ST_Line_Interpolate dont voici la définition (extraite du site www.postgis.fr ) :
Line_Interpolate(LINESTRING, location)
Retourne un point interpolé le long d'une ligne. Le premier argument doit être une LINESTRING. Le second argument est de type float8 dont la valeur doit être comprise entre 0 et 1 et qui représente une fraction de la longueur 2d totale où le point doit être localisé.
Nous allons placer des points tout les 10m le long de chaque contour.Copiez/Collez les requêtes suivante dans l'éditeur de requêtes de PgAdmin III et exécutez les
TRUNCATE TABLE skeleton.voronoi_line;
SELECT skeleton.voronoi('(
SELECT ST_Transform(ST_Line_Interpolate_Point(wkb_geometry,generate_series(10, floor(length)::int, 10)/length),4326) as geom
FROM
(
SELECT ST_Transform(st_exteriorring(wkb_geometry),skeleton.sridUtmByLongitude(wkb_geometry)) as wkb_geometry,
ST_Length(ST_Transform(st_exteriorring(wkb_geometry),skeleton.sridUtmByLongitude(wkb_geometry))) as length
FROM skeleton.water_area
) as a
UNION ALL
SELECT ST_Transform(ST_Line_Interpolate_Point(wkb_geometry,generate_series(10, floor(length)::int, 10)/length),4326) as geom
FROM
(
SELECT ST_Transform(ST_InteriorRingN(wkb_geometry,generate_series(1,ST_NumInteriorRings(wkb_geometry))),skeleton.sridUtmByLongitude(wkb_geometry)) as wkb_geometry,
ST_Length(ST_Transform(ST_InteriorRingN(wkb_geometry,generate_series(1,ST_NumInteriorRings(wkb_geometry))),skeleton.sridUtmByLongitude(wkb_geometry))) as length
FROM skeleton.water_area WHERE id=1
) as b
) as b','b.geom','voronoi_line');
Puis exécutez la requête suivante pour en visualiser le résultat :
Puis enchainons la requête qui va renforcer le squelette.
Cela devient intéressant, le squelette apparait très nettement que ce soit dans le bras le plus étroit comme dans la partie la plus large. Nous allons zoomer sur le bras le plus étroit pour mieux se rendre compte du résultat, en désactivant auparavant l'affichage du diagramme de voronoï.
Nous pouvons constater, que le squelette apparait légèrement en dent de scie, l'application d'une fonction de lissage semble nécessaire, nous allons donc utiliser la fonction skeleton.smoothvoronoiline pour réaliser ce lissage.
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III et exécutez la
DROP TABLE IF EXISTS skeleton.skeleton_line;
CREATE TABLE skeleton.skeleton_line WITH OIDS AS
SELECT a.id,a.geom,st_Length_Spheroid(a.geom,'SPHEROID("WGS 84",6378137,298.257223563)') as longueur,ST_NumPoints(a.geom) as nbpt
FROM
(
SELECT (st_dump(ST_LineMerge(ST_Union(wkb_geometry)))).path[1] as id,skeleton.smoothvoronoiline((st_dump(ST_LineMerge(ST_Union(wkb_geometry)))).geom) as geom
FROM skeleton.voronoi_line
) a;
Puis visualisons le résultat sous OpenJump :
Après le passage de la fonction de lissage, nous obtenons un squelette ou l'effet dent de scie a disparu. Pour avoir une vue d'ensemble du squelette, zoomons sur l'étendue maximale du cours d'eau, regardons ci-dessous le résultat.
Sur cette vue d'ensemble, nous pouvons remarquer la présence de petites branches sur le squelette principale. Nous allons essayer de simplifier encore ce résultat, en éliminant certaines de ces branches. Affichons sous OpenJump les attributs de la table skeleton .skeleton_line qui sont triés sur le critère de la longueur de chaque LINESTRING.
Avant de les supprimer, nous allons afficher les branches candidates à la suppression par le biais de la requête ci-dessous, en fixant le critère à 70m.
SELECT ST_AsBinary(geom),longueur
FROM skeleton.skeleton_line
WHERE id NOT IN(
SELECT a.id
FROM
(
SELECT a.geom,a.id,a.longueur,a.nbpt,(select count(b.*)
FROM skeleton.skeleton_line b
where (Distance(startpoint(a.geom),startpoint(b.geom))=0 or Distance(startpoint(a.geom),endpoint(b.geom))=0))-1 as nbconS,
(SELECT COUNT(b.*) FROM skeleton.skeleton_line b where (Distance(endpoint(a.geom),startpoint(b.geom))=0
or distance(endpoint(a.geom),endpoint(b.geom))=0))-1 as nbconE
FROM skeleton.skeleton_line a
) a
WHERE NOT (a.longueur < 70.0 and a.nbconS=0 or a.nbconE=0)
ORDER BY a.id
);
Copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III
DELETE FROM skeleton.skeleton_line
WHERE id NOT IN(
SELECT a.id
FROM
(
SELECT a.geom,a.id,a.longueur,a.nbpt,(SELECT COUNT(b.*) FROM skeleton.skeleton_line b WHERE (Distance(startpoint(a.geom),startpoint(b.geom))=0 or Distance(startpoint(a.geom),endpoint(b.geom))=0))-1 as nbconS,
(SELECT COUNT(b.*) FROM skeleton.skeleton_line b WHERE (Distance(endpoint(a.geom),startpoint(b.geom))=0 or distance(endpoint(a.geom),endpoint(b.geom))=0))-1 as nbconE
FROM skeleton.skeleton_line a
) a
WHERE NOT (a.longueur < 70.0 AND a.nbconS=0 or a.nbconE=0)
AND a.id
);
Exécutez la jusqu'à ce qu'il n'y ait plus de ligne modifiée.
La requête a été exécutée avec succés : 32 lignes modifiées. La requête a été exécutée en 177 ms.
La requête a été exécutée avec succés : 3 lignes modifiées. La requête a été exécutée en 22 ms.
La requête a été exécutée avec succés : 0 ligne modifiée. La requête a été exécutée en 27 ms.
Puis visualisons le résultat sous OpenJump :
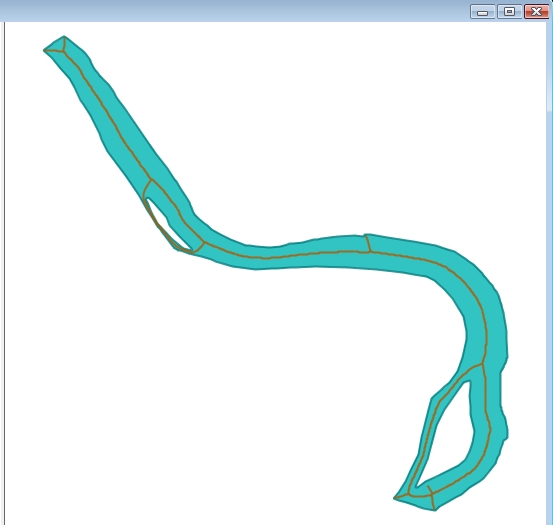
Voila nous y sommes, le squelette est créé, il reste quelques branches qui pourraient être supprimées en augmentant le critère de longueur, pour notre exemple nous nous arrêterons là.
Utilisation du plugin PostGisViewer pour PgAdmin III
Pour la mise en place du plugin je vous renvoie à ce lien :
Plugin PostGisViewer pour PgAdmin III
Une fois la mise en place du plugin effective, si vous utilisez une version de PostgreSQL dont la version est supérieur ou égale à la 9.0, copiez/Collez la requête suivante dans l'éditeur de requêtes de PgAdmin III, exécutez la, puis fermez PgAdmin IIII .
ALTER DATABASE "NOM DE VOTRE BASE" SET bytea_output='escape';
Cette astuce est extraite de l'article « PgAdmin III 1.13 - change in plugin architecture and PostGIS Plugins » dans la partie « PostGIS plugin for displaying geometries in PgAdmin III » dont je vous conseille la lecture.
- Vous pouvez maintenant rouvrir PgAdmin III, copiez/collez la requête suivante dans l'éditeur de requête (un seul éditeur ouvert à la fois)
SELECT st_asbinary(wkb_geometry) as geom,geometrytype(wkb_geometry),id
FROM skeleton.water_area;
SELECT ST_AsBinary(wkb_geometry) as geom,geometrytype(wkb_geometry)
FROM skeleton.voronoi_line;
SELECT ST_AsBinary(geom) as geom, geometrytype(geom),longueur
FROM skeleton.skeleton_line
ORDER BY longueur;
- Dans le navigateur d'objets de PgAdmin, vous devez être positionné sur votre base de données.
- Dans le menu plugins sélectionnez PostGisViewer, vous devriez obtenir ceci :
Sous Map Layers, chaque layer est le résultat d'une requête.
Conclusion
En premier lieu je tiens à remercier :
Georgi Fedoseevich Voronoï, sans qui rien de tout cela ne serait arrivé,
BostonGIS pour ses tutoriels,
Joe Conway pour PL/R, qui a rendu possible la mise en place de cet algorithme,
Postgres OnLine journal pour ses articles,
Refractions Research pour ses développements (PostGIS tout particulièrement),
...
Ce tutoriel est terminé, nous avons vu comment grâce au diagramme de voronoï, réaliser la squelettisation d'un cours d'eau de type POLYGON. L'enchainement de toutes ces requêtes pourrait bien sur être facilement remplacé par une fonction, à qui l'on passerait deux paramètres :
- la géométrie à traiter,
- la tolérance pour la suppression des branches.
A vous de jouer…